Comprendre le monde binaire
Le bit:
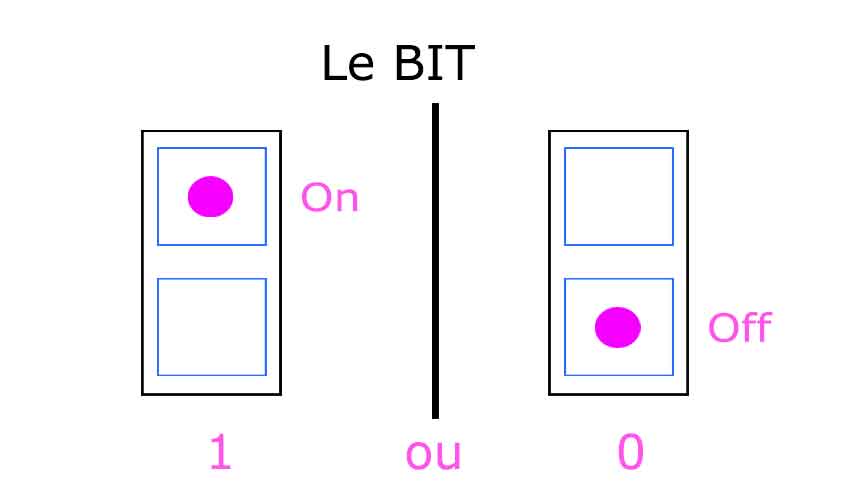
La mémoire de base la plus facile à comprendre est un élément qui
n'a que 2 états : 1 ou
0 on l'apelle le bit.
On peut l'assimiler à un interrupteur qui est soit en position 1 (lumière
allumée) soit en position 0 (lumière éteinte).
C'est un premier pas mais c'est un peu limité : on va déjà devoir agrandir notre mémoire en travaillant avec 2 interrupteurs:
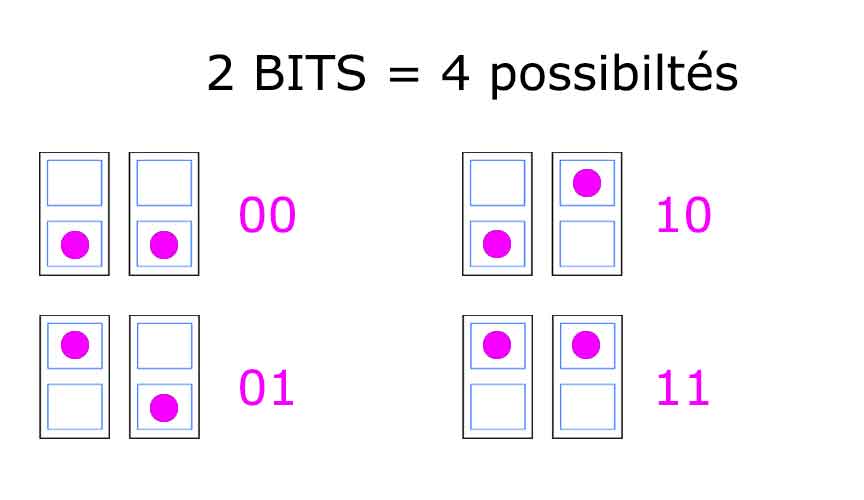
| Le premier interrupteur peut etre en position 0 et le deuxième en position 0 aussi :alors on a : | 0 | 0 |
| Le premier interrupteur peut etre en position 0 et le deuxième en position 1 aussi :alors on a : | 0 | 1 |
| Le premier interrupteur peut etre en position 1 et le deuxième en position 0 aussi :alors on a : | 1 | 0 |
| Le premier interrupteur peut etre en position 1 et le deuxième en position 1 aussi :alors on a : | 1 | 1 |
On a maintenant 4 possibilités.
L'algèbre de Boole
Ceci est un aparté à mon propos car le fait d'avoir choisi
l'image d'un interrupteur permet une compréhension facile mais peut
étre utilsé différemment : notamment pour comprendre l'algèbre de
Boole.
Dans l'algèbre de Boole il y a 2 fonctions primaires :
ET et
OU :
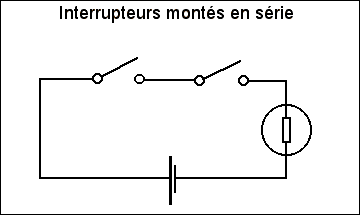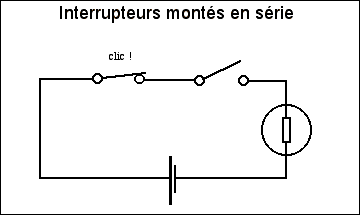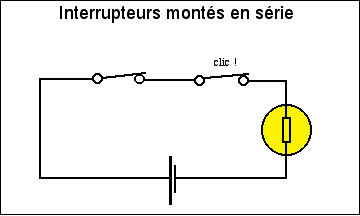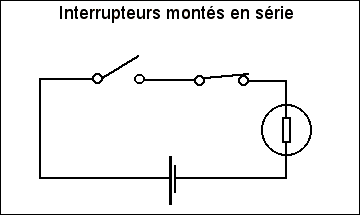
La fonction ET peut etre assimilée à 2 interrupteurs branchés en
série dans un circuit électrique.
Le courant ne pourra passer que si les 2 interrupteurs sont en
position 1.
Si on reprend le tableau ci-dessus on peut en déduire :
| Interrupteur1 | Interrupteur2 | Lumière |
 |
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
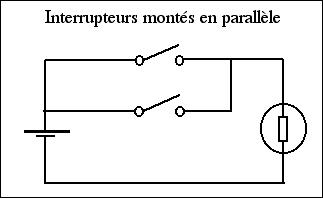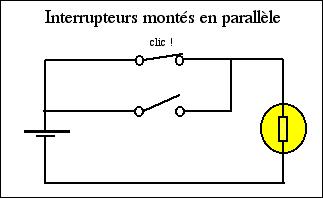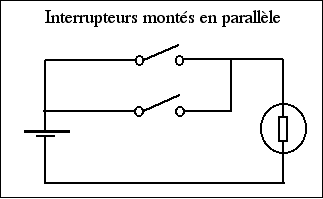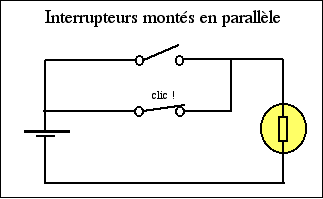
Le courant ne pourra passer que si au moins 1 interrupteur est en position 1.
Si on reprend le même tableau on peut en déduire :
| Interrupteur1 | Interrupteur2 | Lumière |
 |
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 |
On retient que dans les 2 fonctions : 1+1 = 1 alors que ce
n'est pas le cas dans la base binaire.
Fin de l'aparté.
L'octet
Nous évoluons tous dans un monde où le calcul se fait en "base
10" , c'est à dire que nous manipulons des chiffres de 0 à 9.
En travaillant en binaire nous manipulons les chiffres 0 et 1.
On a vu dans le premier paragraphe que si on mettait 2 bits ensemble
on avait 4 possibilités (soit 4 nombres)
Si on met 3 bits ensembles on aura des nombres allant de 000 à 111 ,
soit 8 possibilités.
L'octet (préfixe "oct") est l'assemblage de 8 bits et permet
d'obtenir 256 nombres.
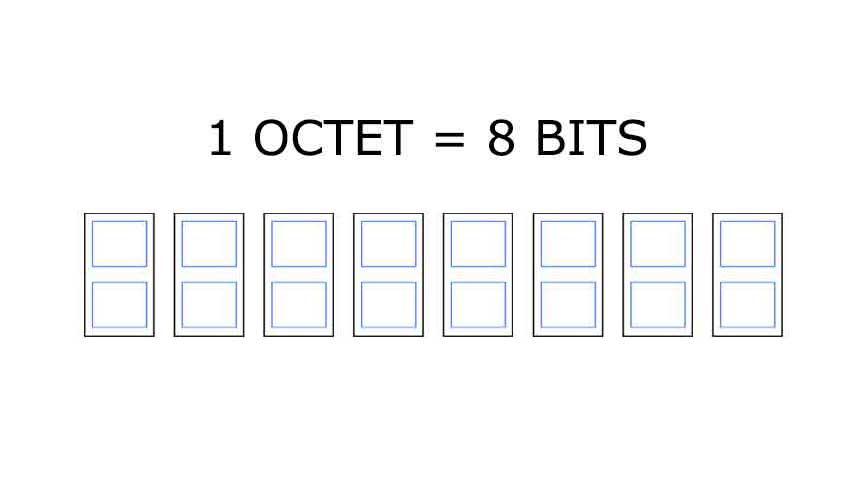
Mais ces nombres vont etre une succession de 8 caractères 0 ou 1 et
ce n'est pas facile à interpréter.
Il faut donc les convertir dans un monde qui nous est familier : la
base décimale :
Exemple : convertir le nombre 01001101 en décimal
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
La valeur obtenue est
26 +
23 +
22 +
20 =
64 + 8 + 4 + 1 = 77.
Dans un octet on peut donc stocker des nombres qui en décimal vont
de 0 à 255
Le code ASCII
Dans cet octet , on a envie de stocker une information qui est
plus "parlante". On s'aperçoit que l'on a 256 possibilités
Il y a 42 caractères dans notre alphabet en majuscule + 42 en
minuscule + 10 chiffres + les caractères spéciaux, il suffit donc
d'affecter un nombre à un caractère : c'est la table de conversion
ASCII (American
Standard Code for
Information Interchange).
Dans le paragraphe précédent nous avons choisit le nombre 77 dans
un octet
Dans la table ASCII le nombre 77 est associé à la lettre "M"
Donc quand vous tapez M sur votre clavier, l'octet se remplit avec
le nombre 77 (en base 10 ou 01001101 en base 2).
Pour le vérifier, ouvrir un éditeur de texte (Word, WordPad)
Cliquez dans une ligne, maintenez la touche ALT enfoncée puis tapez 77 sur le pavé numérique puis relachez la touche ALT
Le caractère M doit apparaitre.
Vous trouverez ci-dessous cette table ASCII qui vous permettra par exemple de taper des caractères spéciaux qui ne sont pas sur votre clavier, par exemple ± en utilisant ALT 241
Table de convertion ASCII
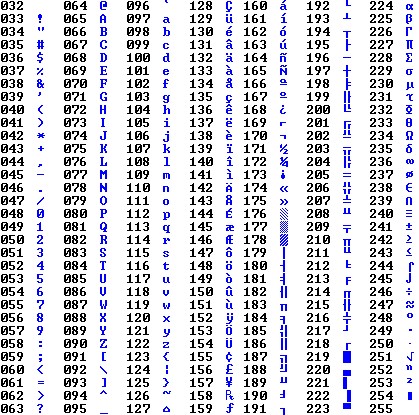
(Les caractères correspondants aux valeurs 0 à 31 sont des caractères spéciaux non imprimables).
Le système hexadécimal
Les
nombres binaires étant de plus en plus longs, il a fallu introduire
une nouvelle base : la base
hexadécimale.
Le système hexadécimal permet d'exprimer des valeurs
comprises entre 0 et 255, en ne posant que deux
caractères.
L’hexadécimal est un système de numération en base 16,
qui utilise les chiffres 0 à 9, avec leurs propres valeurs, et les
lettres A à F pour représenter les valeurs hexadécimales qui
correspondent aux valeurs décimales 10 à 15
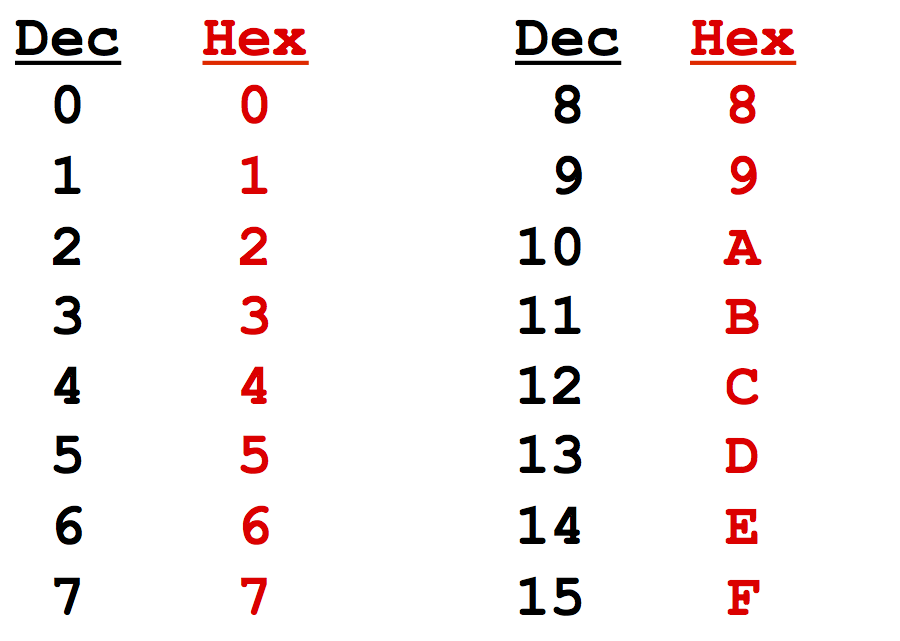
Il s'avère donc particulièrement pratique :
il permet une écriture plus compacte, tout en offrant des techniques
de conversions très simples.Ceci est un avantage pour l'utilisation
en informatique.
Exemple : la valeur décimale 241 = 15 x 16 + 1 = F x16 + 1 se traduira en F1 en valeur hexadécimale
Les systèmes d'exploitation actuel de nos ordinateurs sont des processeurs dits "32 bits" (donc qui gèrent une information contenue dans 4 octets) et les plus modernes sont actuellement en 64 bits.
Dans un système 32 bits, chaque registre peut contenir 32 bits d'information. Cela signifie qu'il peut stocker des nombres entiers allant de 0 à 2^32-1, ce qui équivaut à environ 4 milliards de valeurs différentes. Les instructions et les données sont stockées en mémoire sous forme de nombres binaires à 32 bits.
Cependant, les processeurs 64 bits offrent des avantages tels que la possibilité de gérer des quantités de mémoire plus importantes, ce qui est utile pour les applications de traitement de données lourdes telles que l'infographie, la vidéo et les jeux vidéo en haute résolution. Les processeurs 64 bits peuvent également traiter des instructions plus complexes plus rapidement que les processeurs 32 bits, ce qui les rend plus adaptés aux tâches de calcul intensif.
En résumé, comprendre le monde binaire est essentiel pour comprendre le fonctionnement des ordinateurs et de la technologie numérique en général. En utilisant des bits, des fonctions logiques et des octets, les ordinateurs peuvent stocker et manipuler des informations à des vitesses incroyables, nous permettant d'accéder à une quantité énorme de données et de ressources en ligne.
Cette page a été mise à jour le 24/02/2023
